<< radio home
<< index
by disinfoniacs #69 & #1
>>>>
Ohm's law is a fundamental principle in the world of electronics that explains the relationship between voltage, current, and resistance. Simply put, Ohm's law states that the current flowing through a conductor between two points is directly proportional to the voltage across those points and inversely proportional to the resistance between them.
In practical terms, this means that if you increase the voltage across a circuit, the current will also increase, provided that the resistance remains constant. Similarly, if you increase the resistance, the current will decrease, provided that the voltage remains constant. This relationship can be expressed mathematically as I = V/R, where I is the current, V is the voltage, and R is the resistance.
To use Ohm's law to calculate the current flowing through a circuit, you first need to know the voltage and resistance of the circuit. Once you have these values, simply divide the voltage by the resistance to obtain the current. For example, if you have a circuit with a voltage of 12 volts and a resistance of 4 ohms, the current flowing through the circuit would be 3 amps (I = 12V / 4Ω = 3A).
You can also use Ohm's law to calculate the voltage across a circuit if you know the current and resistance. To do this, simply multiply the current by the resistance to obtain the voltage. For example, if you have a circuit with a current of 2 amps and a resistance of 5 ohms, the voltage across the circuit would be 10 volts (V = 2A x 5Ω = 10V).
Finally, you can use Ohm's law to calculate the resistance of a circuit if you know the voltage and current. To do this, simply divide the voltage by the current to obtain the resistance. For example, if you have a circuit with a voltage of 6 volts and a current of 2 amps, the resistance of the circuit would be 3 ohms (R = 6V / 2A = 3Ω).

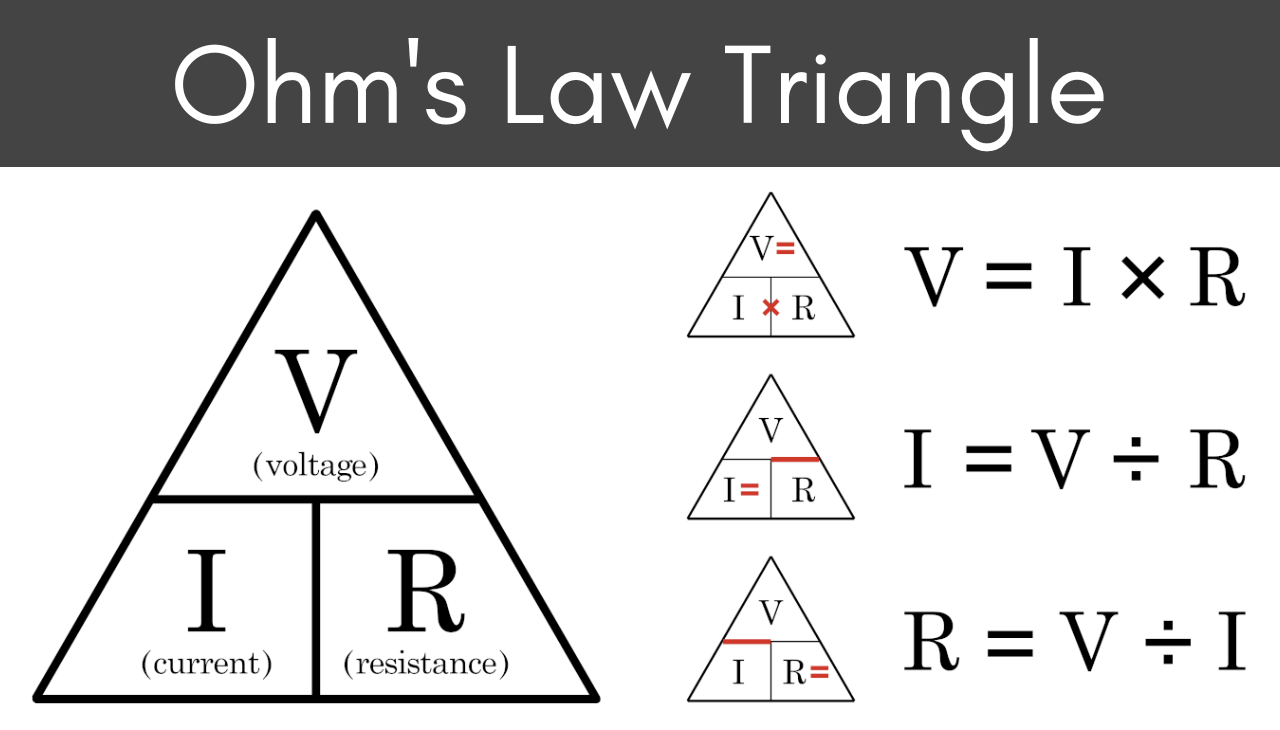
Ohm's Law can be easily calculated using a triangle, which is known as the Ohm's Law triangle or the EIR triangle. The triangle helps in finding the value of any two of the three variables involved in Ohm's Law, given the value of the third variable.
The triangle has three sections, with the letters E, I, and R written in each of them. The letter E represents voltage or electromotive force, I represents current, and R represents resistance. The triangle can be used to calculate the value of any two variables using the following formulas:
To use the Ohm's Law triangle, simply cover up the letter that represents the variable you want to find, and the remaining two variables and their corresponding units will form a formula. Then, rearrange the formula to find the desired variable.
For example, suppose you want to find the current in a circuit with a voltage of 12 volts and a resistance of 4 ohms. To do this using the Ohm's Law triangle, cover up the I section, and you will be left with E over R. Then, substitute the values of voltage and resistance into the formula, and calculate the result:
Thus, the current flowing in the circuit is 3 amperes.
The Ohm's Law triangle is a simple and intuitive tool for calculating the values of voltage, current, and resistance in a circuit. With a basic understanding of the formulas involved, anyone can use this method to quickly and easily solve electrical problems.
<< previous lesson | next lesson >>
---
<< radio home
<< index
