<< radio home
<< index
by disinfoniacs #69 & #1
>>>>
As we delve into the arcane depths of antenna esoterica, let us not forget the fundamentals we explored in Lesson 3, where we traversed the labyrinthine world of radio wave characteristics, dissecting polarization, frequency, and wavelength. Fear not, dear reader, for we shall revisit these principles in the ensuing discussion, so brace yourself for a thrilling journey into the shadows of radio theory.

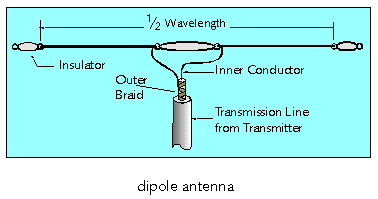
Among the simplest of antenna constructions, the humble dipole antenna stands proud, an exemplar of elegant minimalism. A classic half-wave dipole takes the form of a single wire, or straight line, bisected by the feed line, creating the iconic "T" shape reminiscent of a tenuous bridge between ethereal realms.
The positioning of your dipole is the key to unlocking its polarization potential. Envision, if you will, a T-shaped antenna suspended between two arboreal guardians in your own backyard, the dipole oriented parallel to the very surface of our terrestrial plane. In this configuration, the antenna achieves horizontal polarization. Radiating its most potent signals broadside, a half-wave dipole with its wires traversing the north-south axis will emit the strongest signals to the east and west.
Were you to contort the antenna, its elements ascending and descending in a vertical orientation, it would transform into a vertically polarized antenna, its nature forever altered by your intervention.
Resonance, that most elusive and enigmatic quality, can be tamed by adjusting the dipole's length to accommodate the desired frequency or band. Bear in mind the inverse relationship between frequency and wavelength: as frequency soars to greater heights, wavelength dwindles accordingly. To attune a dipole antenna to a higher frequency, one need only truncate its length.
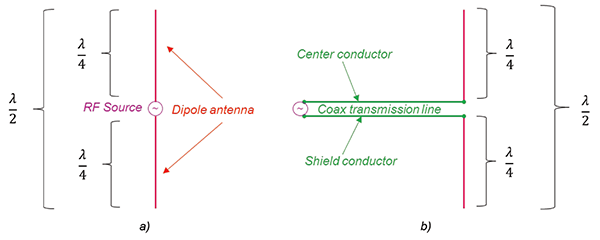
Let us ponder two examples of calculating antenna lengths for distinct bands. In the first scenario, we seek to forge a quarter-wavelength vertical antenna resonant at 146 MHz. To determine the approximate length, we must invoke the hallowed formula: Wavelength = 300 / Frequency in MHz
Next, we shall endeavor to calculate the length of a half-wavelength 6-meter dipole. This task is delightfully simple:
In both instances, we employed approximate lengths, as a multitude of factors beyond the scope of the exam come into play, such as the metal employed, the antenna's elevation above the ground, and other elusive elements.
At times, physical constraints may prevent you from extending or contracting your antenna to the desired length. In such cases, the resonant frequency can be altered by employing an antenna loading coil, an ingenious inductor that permits electrical elongation by integrating inductors within the radiating elements. A popular portable antenna leverages this principle to achieve resonance across a range of frequencies.
Reflecting on our 2-meter calculation, we derived the length of a quarter-wavelength dipole. In the realm of VHF and UHF, the intrepid ham radio operator may uncover the advantages of employing a properly mounted 5/8-wavelength antenna, as it boasts a lower radiation angle and superior gain when compared to its 1/4-wavelength counterpart. Such an antenna, meticulously crafted and positioned, serves as a formidable weapon in the never-ending battle for clear and efficient communication amidst the cacophony of electromagnetic waves that permeate the airwaves.
Thus, dear reader, we have ventured through the twisting passages of antenna theory, expanding our understanding of the delicate interplay between frequency, wavelength, and polarization. With this newfound knowledge, you are now better equipped to navigate the mysterious world of amateur radio, forging connections across vast distances and transcending the boundaries of space and time.
<< previous lesson | next lesson >>
---
<< radio home
<< index
